Bewertung:
Derzeit gibt es keine Leserbewertungen. Die Bewertung basiert auf 2 Stimmen.
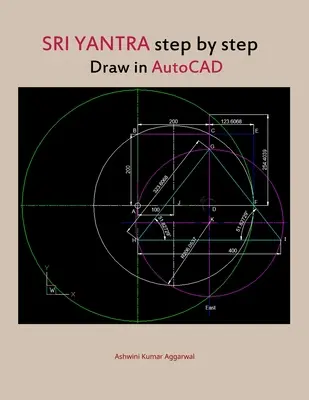
Sri Yantra step by step draw in AutoCAD
Ein mit Sorgfalt und Präzision gestaltetes Sri Yantra ist kostbar, schön und sehr wohlwollend. Um mit dem Zeichnen zu beginnen, verwenden Sie eine 2D-Entwurfssoftware, z. B. AutoCAD, BricsCAD, nanoCAD, LibreCAD usw.
⬤ Stellen Sie die Genauigkeit der Bemaßung auf vierDezimalstellen ein, z. B. 0. 0000.
⬤ Messen Sie bei jeder gezeichneten Linie, jedem gezeichneten Winkel oder Kreis, ob die Bemaßung genau übereinstimmt.
⬤ Selbst ein kleiner Fehler lässt das Sri Yantra seine Schönheit und Kostbarkeit verlieren.
⬤ 1 Quadrat ABCD, Seite 200.
⬤ 2 Halbiere das Quadrat bei J,.
⬤ Erstelle ein rechtwinkliges Dreieck JCD mit der Hypotenuse JC = 223. 6068, Winkel CJD = 63. 4349.
⬤ 3 Zeichne einen schwarzen Kreis mit Mittelpunkt bei J, Radius = Hypotenuse JC = 223. 6068.
⬤ 4 Erweitern Sie das Quadrat ABCD zu einem Rechteck ABEF, wobei die längere Seite AF = BE = 323. 6068.
⬤ 5 Zeichne einen grünen Kreis mit Mittelpunkt bei A, Radius = 323. 6068.
⬤ 6 Verlängere die Seite des Quadrats DC so, dass sie den grünen Kreis im oberen Punkt g berührt. Die Länge Dg = 254. 4039.
⬤ Für die Exaktheit,.
⬤ Erweitern Sie die Seite des Quadrats CD so, dass sie den grünen Kreis im unteren Punkt berührt. Diese Länge = 254. 4039.
⬤ Diese beiden Längen müssen gleich sein. Dies dient nur zur Überprüfung, ob wir bisher richtig vorgegangen sind.
⬤ Wenn beide Längen gleich sind, haben wir den Scheitelpunkt g für unser Dreieck T1u gefunden.
⬤ 7 Nun verbindeA mit g, und wir erhalten die Seite Ag unseres Dreiecks im Goldenen Schnitt T1u.
⬤ Beachte, dass Seite Ag = Radius des grünen Kreises = 323. 6068
⬤ 8 Kopiere und spiegle die Seite Ag, um die Seite gi des Dreiecks im Goldenen Schnitt zu erhalten.
⬤ 9 Verbinde die Punkte A bis i, um die Basis Ai des Dreiecks im Goldenen Schnitt T1u zu erhalten.
Das größte Dreieck mit dem Scheitelpunkt nach oben ist der Startpunkt für das Sri Yantra.
⬤ Abmessungen für Golden Ratio Triangle T1u = Agi müssen genau sein
⬤ Grundlinienlänge = 400.
⬤ Jede gleichschenklige Seitenlänge = 323. 6068.
⬤ Jeder gleichschenklige Winkel = 51. 82729.
| ISBN: | 9789395766623 |
| Autor: | |
| Verlag: | |
| Sprache: | Englisch |
| Einband: | Taschenbuch |
Derzeit verfügbar, auf Lager.
